|
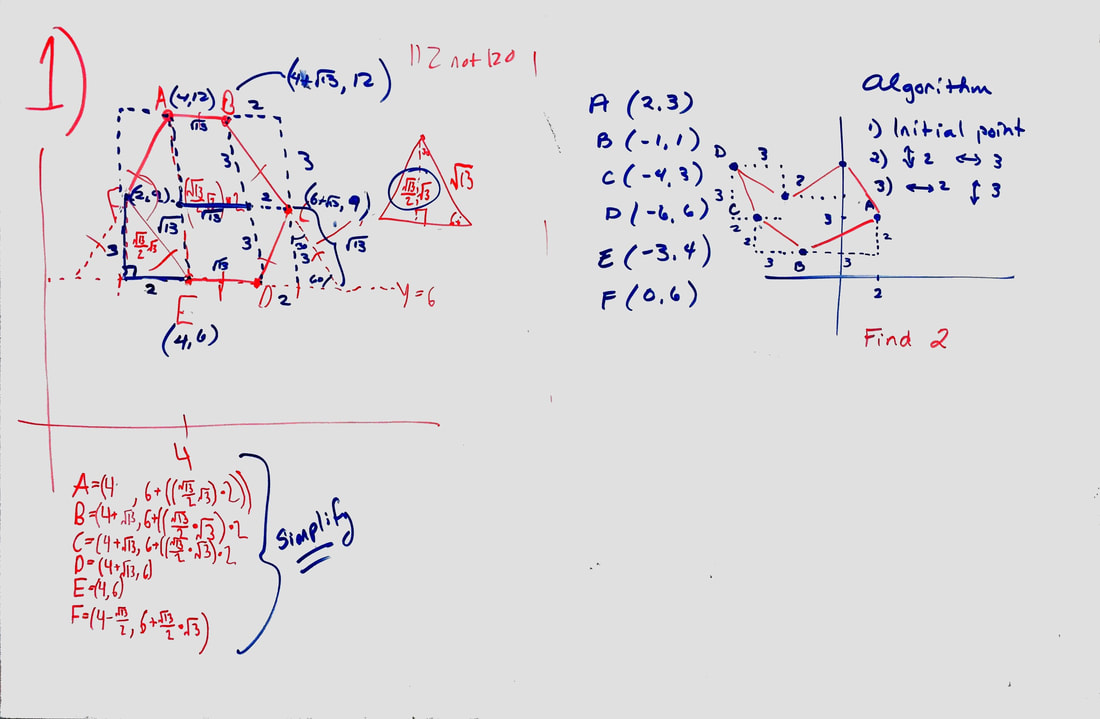
When we give students the space to create their own meanings and understandings, marvelous things happen. Her is a problem on a recent problem set: Find an example of an equilateral hexagon whose sides are sqrt(13) units long. Give the coordinates for all for all six points. In class we looked at three different solutions strategies...
1. Start at point (a,b) and count "over 2, up 3" to find the next point. At some point we needed to a horizontal translation of sqrt(13) to get to the next point. As a result, the points were in radical form. 2. Start at point (a,b) and assume the hexagon is regular and the side relationship of a 30-60-90 triangle to find the sides. Again the points are in radical form. 3. One student wanted integer coordinates. We had previously talked about lattice points. After some experimentation with "horizontal 2, vertical 3" and/or "vertical 2 horizontal 3" on GeoGebra they found a solution that was not convex!
0 Comments
|
Author"Your only as good as your record collection." -DJ Spooky Archives
September 2020
Categories |
 RSS Feed
RSS Feed
